Физико-химические процессы в аквариуме значительно сложнее, чем это представляют себе любители, а для того, чтобы разобраться в этом детально нужны фундаментальные знания в химии, физике и математике. Кроме того, всё это неразрывно связано с биологическими особенностями тех или иных аквариумных систем, что только усложняет задачи анализа и правильного понимания. Я уже кратко писал об этом в своих статьях в Аквариумисте, книгах и других публикациях. Добавляя в воду лекарства, те или иные химические вещества надо реально представлять себе, что при этом происходит, хотя в большинстве случаев всё это ещё недостаточно изучено. К сожалению, подавляющее большинство моих читателей не слишком хорошо подготовлены в химии и математике, чтобы понимать то, о чём идёт речь, даже в простейших случаях и именно поэтому в своих книгах и статьях я избегаю химических и математических формул. Рассказывая в своё время детям и взрослым об аквариумах в теле- и радиопередачах, я старался говорить на понятном всем языке, за что руководитель моей диссертационный работы (замечательный человек!) не раз меня укорял. Он говорил, - "Серёжа ты ведь уже настоящий учёный и, пожалуйста, старайся выражаться, как у нас принято, то есть с использованием всего спектра научной терминологии”. На своих аквариумных лекциях я пробовал применять термины, но по кислым лица слушающих сразу понял, что делать этого нельзя. В период работы в своём НИИ Приборостроения, а потом в качестве специалиста по аквариумам и за границей мне довелось пользоваться самыми современными на тот период приборами и установками, позволяющими прояснить кое-какие интересные моменты на которые я не мог найти ответов ни в одной аквариумной книге. .При этом очень важно было так сформулировать свой вопрос таким образом, чтобы в
рамках имеющейся аппаратуры для проведения экспериментов, буквально в
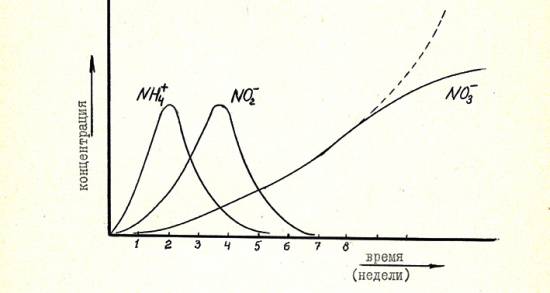
цифрах получить однозначный ответ. Эксперимент 1. Рассмотрим, например, вопрос изменения активной реакции воды рН при добавлении в воду нерестового водоёма кислоты, пускай, как мы привыкли, ортофосфорной. Просто вливаем и перемешиваем. Прецизионные измерения с использованием предварительно калиброванных измерительных электродов показывают, что при этом рН быстро в течение нескольких секунд, иногда минут, стремительно снижается до заданных параметров. А вот потом начинается самое интересное - концентрация водородных ионов начинает плавно в течение десятков минут возвращаться к исходному значению вследствие, как принято говорить у химиков, низкой буферной ёмкости раствора. Для аквариумистов-разводчиков это означает не что иное, как нестабильность заданных параметров воды и объяснение одной из причин возможных неудач. Эксперимент 2 Другой пример, который будет интересен любителям растений связан с добавлением в воду такого важного элемента, как марганца. Для простоты эксперимента я добавлял в воду обычную марганцовку - перманганат калия, а процессы рассматривал с точки зрения изменения окислительно-восстановительного потенциала RH. Измерения проводил и использованием специальных платиновых электродов (тоже предварительно проверенных) на которых, как известно возникает потенциал водорода, подлежащий измерению и последующему анализу. Как и в предыдущем случае вливал в воду аквариума раствор перманганата и перемешал. В течение нескольких секунд окислительно-восстановительный потенциал воды резко возрос (напомню,что в предыдущем эксперименте величина рН уменьшилась), а затем стал быстро в течение примерно получаса возвращаться к исходному уровню. Однако причина в данном случае явно другая - перманганат стал окислять имеющуюся в воде органику, что привело к снижению RH. Хочу отметить, что и в том и в другом случае для наглядности данные фиксировались самописцем (Хьюлет-Паккард), а сам характер записей был зеркальным отображением друг-друга. Образно выражаясь, добавляя реагенты, мы подвергали воду в системе импульсному воздействию и получили характерную ответную реакцию. Давайте усложним вопрос и в качестве примера рассмотрим и проанализируем ещё один простейший случай, когда я писал о содержании водяных черепах. Здесь все проблемы прежде всего сводятся к тому, чтобы избежать чрезмерного и быстрого загрязнения биологического фильтра. Рекомендация предельно проста - понаблюдайте за черепахами и определите, через какое время после кормления она испражняется и подхватите фекалии сачком, чтобы не перегружать фильтр. В моих книгах вы найдёте простейшую схематичную картинку о чередовании процессов нитрификации (см фото ниже), а теперь давайте оценим с точки зрения математического анализа процесс выделения фекалий, как единичный импульс. Вот черепашка (рыбка, креветка или пускай даже бегемот) покакали. Это означает, что в воду аквариума, а затем в систему фильтрации в определённый момент времени попало конечное количество материала, который будут перерабатывать автотрофные и нитрифицирующие гетеротрофные бактерии. Процессы это, как видно из графиков явно нелинейные, но не трудно их линеаризовать, то есть применить кусочно-линейную аппроксимацию для того, чтобы можно было применить интеграл Дюамеля с последующей суперпозицией. Кстати, для примера я выбрал далеко не новый метод для анализа - знаменитый французский математик Жан Мари Констан Дюамель родился ещё в 1797 году. Возвращаясь к анализу, входной сигнал системы описывается некоторой функцией где В случае, если входной сигнал составной и функция Отклик на остальных интервалах вычисляется по формулам, вытекающих из принципа суперпозиции:
Источник: http://www.aquariumist.ru/publ/ob_akvariume_chut_serjoznee/25-1-0-445 | |
|
| |
| Просмотров: 4289 | |
| Всего комментариев: 0 | |




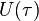 , где
, где  независимая переменная, реакция системы на этот сигнал выражается формулой
независимая переменная, реакция системы на этот сигнал выражается формулой
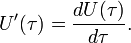
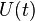 испытывает разрывы (например, в моменты времени
испытывает разрывы (например, в моменты времени 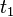 ,
, 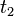 ), то вышеуказанная формула справедлива только на интервале [0,
), то вышеуказанная формула справедлива только на интервале [0, 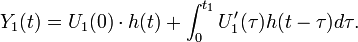
![Y_2(t)= Y_1(t) + \left[ U_2(t_1)-U_1(t_1) \right] \cdot h(t-t_1) + \int_{t_1}^{t_2} U_2'(\tau)h(t-\tau)d\tau;](http://upload.wikimedia.org/math/d/c/b/dcb0dc506f71bff5db2f6e79a4627f24.png)
![Y_3(t)= Y_2(t) +\left[ U_3(t_2)-U_2(t_2) \right] \cdot h(t-t_2) + \int_{t_2}^{\mathcal{1}} U_3'(\tau)h(t-\tau)d\tau;](http://upload.wikimedia.org/math/5/c/7/5c7fd988a39ab4a4d328a91443466c1b.png)


